221. Maximal Square (Medium) Facebook Apple Airbnb

Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

For example, given the following matrix:

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Return 4.

https://leetcode.com/articles/maximal-square/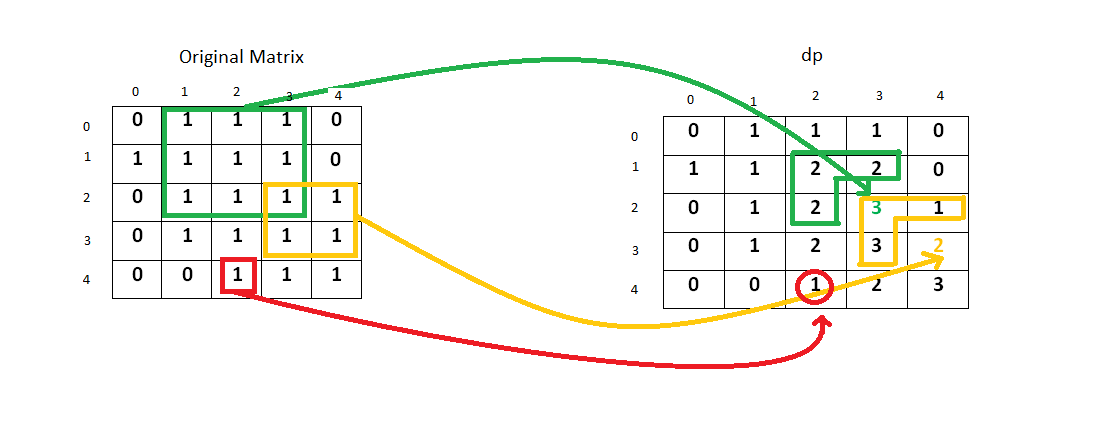Solution 1: DP O(m * n); O(m * n)

    /**
     * DP O(mn);O(mn)
     * state: dp(i,j) represents the side length of the maximum square whose bottom right corner is 
     * the cell at index (i,j) in the original matrix.
     * dp(i, j)= min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1))+1
     */
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return 0;
        }

        int m = matrix.length;
        int n = matrix[0].length;
        int[][] dp = new int[m + 1][n + 1];
        //不建议在这里初始化第0行和第0列，可以在下面的循环中一起赋值，大大节省代码量，但这样做记得要将数组各加一行一列。

        int max = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (matrix[i - 1][j - 1] == '1') {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) + 1;
                    max = Math.max(max, dp[i][j]);
                }
            }
        }
        return max * max;
    }

Solution 2: DP O(m * n); O(n)

    /**
     * DP O(mn);O(m)
     * As can be seen, each time when we update size[i][j], we only need size[i][j - 1], size[i - 1][j - 1]
     * (at the previous left column) and size[i - 1][j] (at the current column).
     * So we do not need to maintain the full m*n matrix. In fact, keeping two columns is enough.
     * Now we have the following optimized solution.
     */
    public int maximalSquareB(char[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return 0;
        }
        int[] dp = new int[matrix[0].length + 1]; //n, not m
        int pre = 0;

        int max = 0;
        for (int i = 1; i <= matrix.length; i++) {
            for (int j = 1; j <= matrix[0].length; j++) {
                int temp = dp[j];
                if (matrix[i - 1][j - 1] == '1') {
                    dp[j] = Math.min(Math.min(dp[j - 1], pre), dp[j]) + 1;
                    max = Math.max(max, dp[j]);
                } else {
                    dp[j] = 0;
                }
                pre = temp;
            }
        }
        return max * max;
    }

Follow Up:

1.让你找出 最大的square with chess pattern的边长，chess pattern：一个正方形中，条对角线全为0或者1，其余元素相反。
http://www.1point3acres.com/bbs/thread-309917-1-1.html

1 0 1 1 0
0 1 0 1 0
1 0 1 1 1
最大的chess pattern如下：
1 0 1
0 1 0
1 0 1

    public int maximalSquareC(char[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[][] dp = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                dp[i][j] = 1;
            }
        }

        int max = 0;
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < m; j++) {
                if (matrix[i][j] == 1) {
                    if (matrix[i - 1][j - 1] != 1 || matrix[i - 1][j] != 0 || matrix[i][j - 1] != 0) {
                        continue;
                    }
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    max = Math.max(max, dp[i][j]);
                }
                if (matrix[i][j] == 0) {
                    if (matrix[i - 1][j - 1] != 0 || matrix[i - 1][j] != 1 || matrix[i][j - 1] != 1) {
                        continue;
                    }
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    max = Math.max(max, dp[i][j]);
                }
            }
        }
        return max;
    }